海面模拟（一）

  这一篇文章将作为海面渲染的最终篇。第四篇已经介绍了基于FFT的海面渲染的一般步骤，并介绍了基于Phillips频谱的海面高度偏移和水平偏移的过程，介绍了FFT蝶形变换的实际原理和实现它的方法，同时介绍了如何使用ComputeShader实现这一过程，最后介绍了海面网格的生成方法，其中包括基础的海面网格生成方法，Skirt-Mesh的生成过程。对于海面网格的渲染方法，只介绍了如何对海面网格的顶点进行偏移，更多的渲染内容没做介绍。

  这一篇文章将会介绍基于Jonswap频谱的海面网格的实现方法，结合论文[1]中的公式和一份开源代码进行介绍。开源代码的地址会附在参考文献中。最后对五篇文章进行总结。关于海面网格的生成，FFT的内容就不再着墨，可以参考第四篇的介绍。

  本篇文章不会对原论文内容进行过多地解读，有渠道的朋友可以自己下载论文阅读和研究。不过结合这篇文章和提供的开源代码，可以更好地理解论文中给出的公式。开源代码可以认为是对论文的复现，但是又略有差异。也有可能是我本人也没有把原论文完全精度导致理解上有偏差。

基于Jonswap频谱的海面渲染方法

  在github上有一个Unity工程，链接附在后面。在该工程中，基本实现了论文[1]中的内容。在这里就结合这两份资料来进行介绍。

  代码的目录结构如下，其中ComputeShaders里存着的是FFT和IFFT相关的代码（有一点问题，后面再说）。Resources里保存的是使用的噪声贴图。Scripts里保存的是所有相关的C#脚本，实现了网格生成，ComputeShader的调度和使用等逻辑。Shaders里只有一个渲染海面网格的Shader。

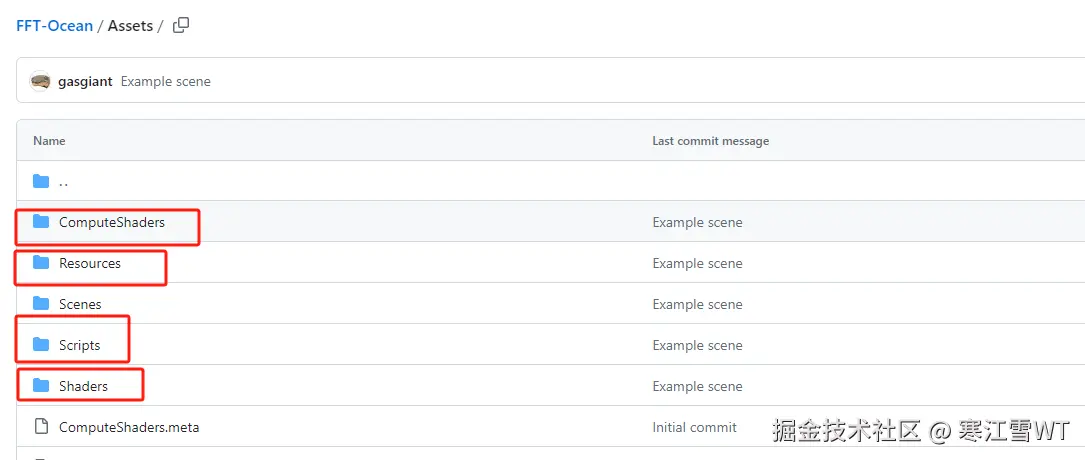
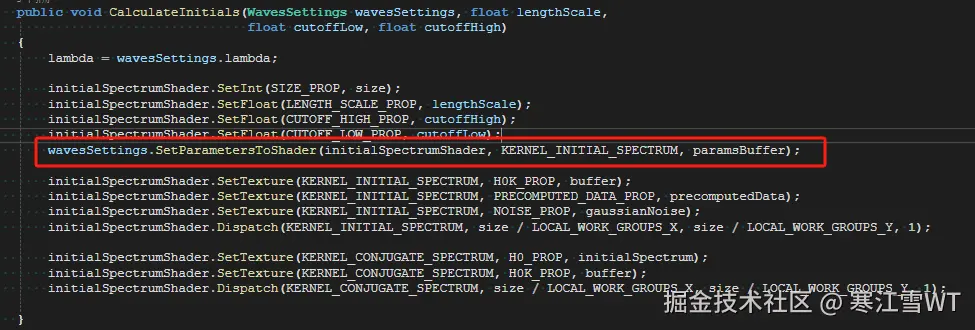
  在Assets目录下，还有一个Waves Setting的配置，该配置的内容是用于生成初始频谱的参数。

初始频谱$h_0(\vec{k})$的生成

  初始频谱的生成过程，涉及到的公式包括：JONSWAP频谱，哈塞尔曼方向扩展，短波过滤盒频率导数。

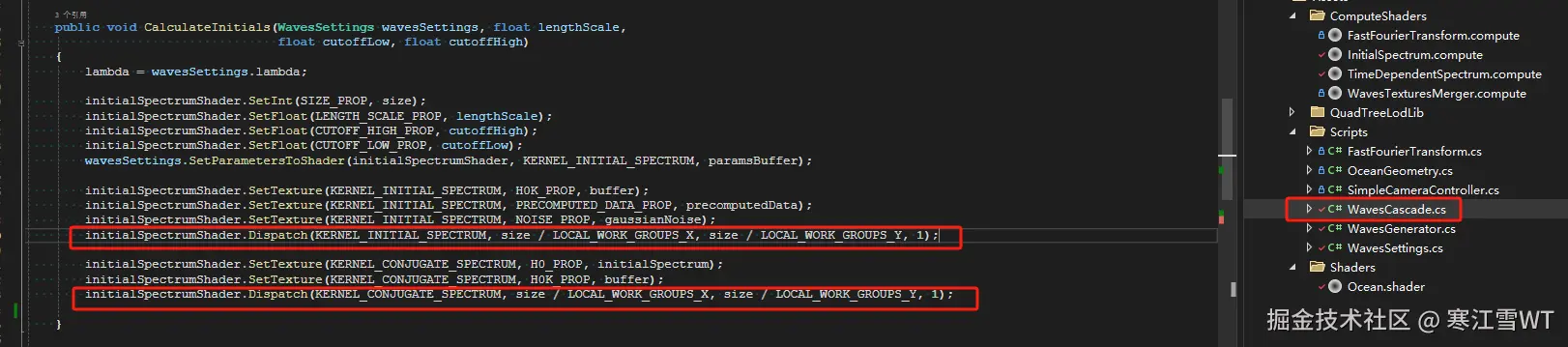
  在代码中，该过程的实现在WavesCascade.cs文件中的CalculateInitials方法内。

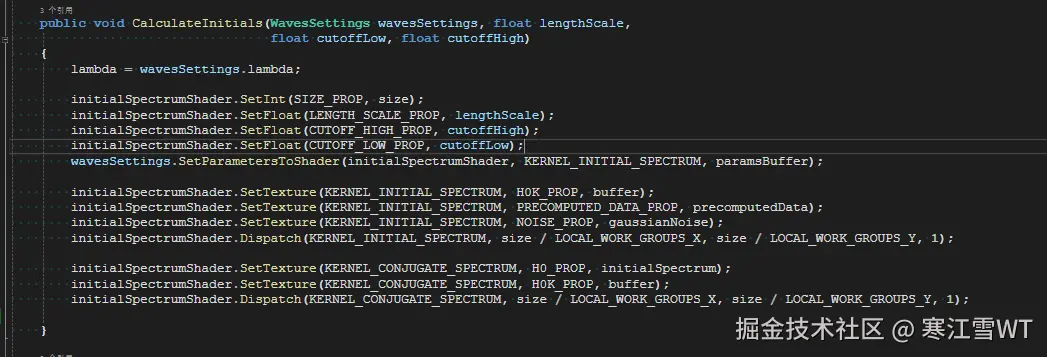
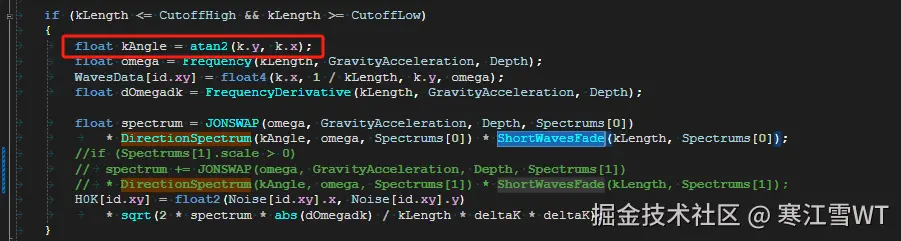
角度频率及其导数

  角度频率$\omega$及其导数$d\omega_k$的计算公式如下：

$$\omega=\sqrt{g|\vec{k}|tanh(min(|\vec{k}|d,20))}\\ d\omega_k=\frac{g\left\{\frac{|\vec{k}|d}{cosh^2(|\vec{k}|d)}+tanh(min(|\vec{k}|d,20)\right\}}{2\omega}\\ \vec{k}=(\frac{2\pi(x-Size/2)}{LengthScale},\frac{2\pi(y-Size/2)}{LengthScale})$$

  $\vec{k}$的计算和第四篇中的一致，就不再说明。该公式是根据代码的实现来写的，看代码比较简洁，代码的实现如下：

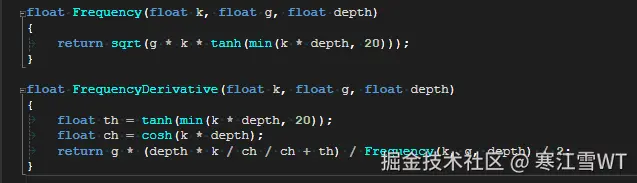
  在开始执行初始化频谱的过程时，会首先计算$\omega$和$d\omega_k$。$\omega$在后续的公式中用得比较多，$d\omega_k$在最后一步使用。

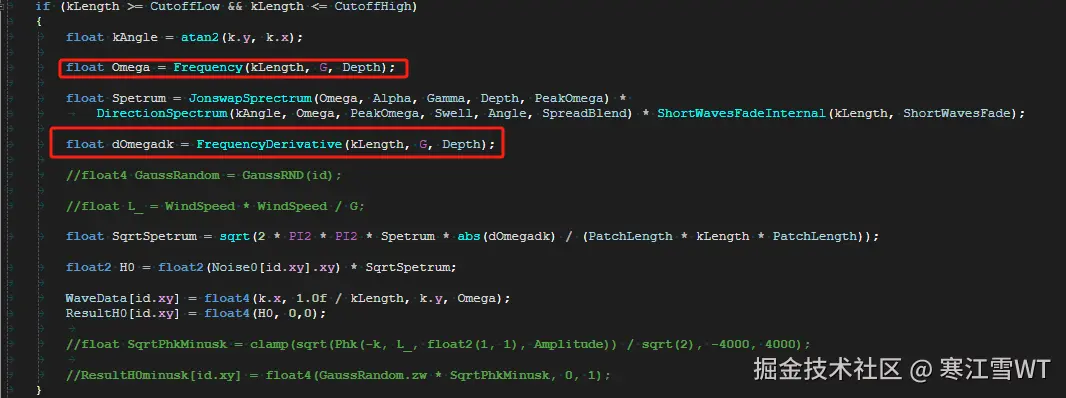
JONSWAP频谱公式

  JONSWAP频谱公式如下：

$$S_{JONSWAP}(\omega)=\frac{\alpha g^2}{\omega^5}\exp(-\frac{5}{4}(\frac{\omega_p}{\omega})^4)\gamma^r\\ r=exp(-\frac{(\omega-\omega_p)^2}{2\sigma^2(\omega_p)^2})\\ \gamma=3.3\\ \alpha=0.076(\frac{U^2}{Fg})^{-0.22}\\ \omega_p=22(\frac{g^2}{UF})\\ \sigma= \left\{ \begin{aligned} &0.07\quad\omega\leq\omega_p\\ &0.09\quad\omega\gt\omega_p\\ \end{aligned}\\ \right.$$

  该公式的参数非常多，没有办法一一讲解，如果本着纯抄公式去实现的初心去看的话，只需要按公式去计算即可。在具体的实现中，由外部传入的参数包括：

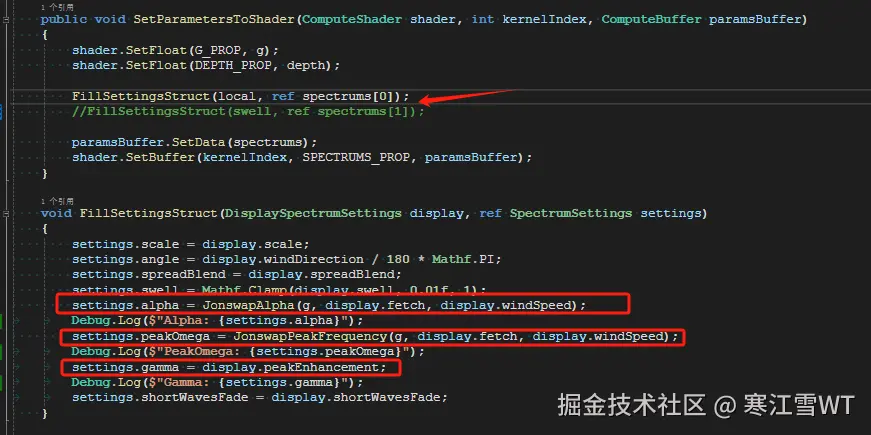
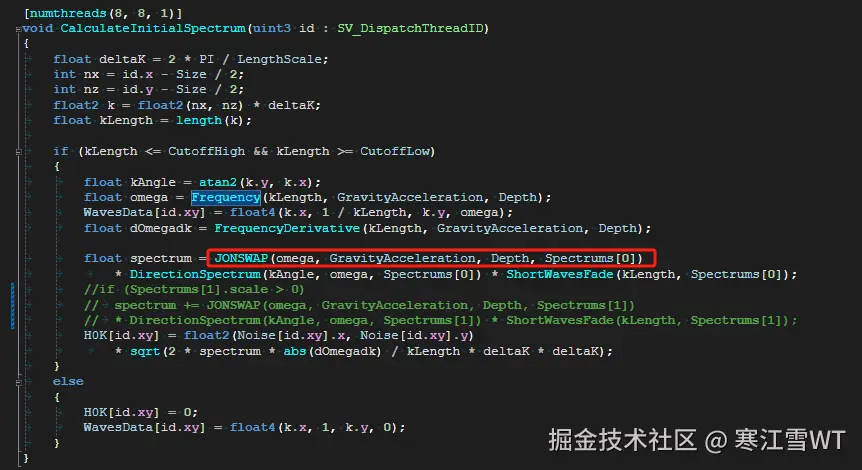
$\gamma,\omega_p,\alpha$。这在代码中有所体现，在下图中红框内的代码是设置这些参数的调用。

  这一段代码里，计算了$\gamma,\omega_p,\alpha$。可以看到，$\gamma$是手动配置得到的，而$\omega_p,\alpha$还要经过计算，计算使用的参数是手动配置的。

  $\alpha$的计算公式如下，其中g是重力加速度9.81。U在配置项中，被标记为Fetch，论文中解释为平均风速，F是风速。

$$\alpha=0.076(\frac{U^2}{Fg})^{-0.22}$$

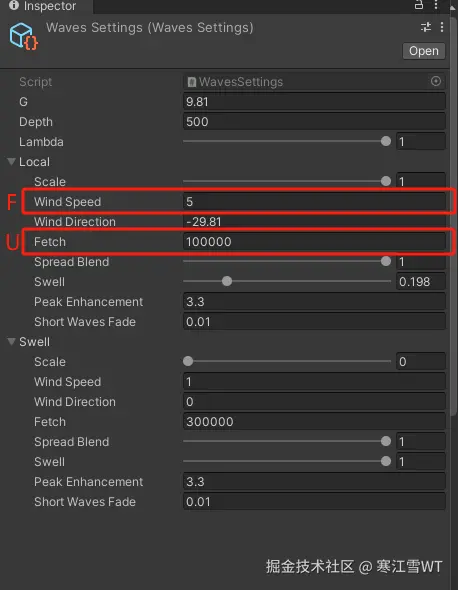
  $\omega_p$的计算公式如下，其中g是重力加速度，U和F同上。

$$\omega_p=22(\frac{g^2}{UF})$$

  根据论文的介绍，公式$S_{JONSWAP}(\omega)$仅仅表示了深水频谱，Kitaigorodskii和Huge等人提出了一种频率依赖函数，作为深水频谱的修正。该公式如下：

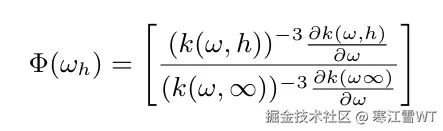
  在代码中，使用的是它的近似公式：

$$\Phi(\omega,h)= \left\{ \begin{aligned} \frac{1}{2}(\omega_h)^2\qquad if\quad\omega_h\leq1\\ 1-\frac{1}{2}(2-\omega_h)^2\qquad if\quad\omega_h\gt1 \end{aligned} \right.$$

  将这两个公式的结果相乘作为第一部分的结果，称为非方向性频率函数（non-directional spectrum function）

$$S_{TMA}(\omega) =S_{JONSWAP}(\omega) ( h)$$

  代码中关于这部分的实现，可以看InitialSpectrum.compute中，红框部分的函数：

哈塞尔曼方向扩展（Hasselmann Directional Spreading)

  方向扩展函数的公式可以总结如下：

$$s=s_p(\omega,\omega_p)+s_{\xi}\\ s_p(\omega,\omega_p)= \left\{ \begin{aligned} &9.77 (\frac{\omega}{\omega_p})^{-2.5}&\qquad if\quad\omega\leq\omega_p\\ &6.97 (\frac{\omega}{\omega_p})^{5}&\qquad if\quad\omega\gt\omega_p\\ \end{aligned} \right.\\ s_{\xi}=16tanh(\frac{\omega_p}{\omega})*\xi^2\\ D_\xi(\omega,\theta)=Normalize(s)|cos(\frac{1}{2}\theta)|^{2s}\\ \theta=atan2(k.y,k.x)\\$$

  在上式中，$\xi$是由外部传入的一个极小值。$k$的计算，和上一篇文章介绍的Phillips的计算一致，这里$\theta$的计算与$k$有关。在代码中，还有一个插值的操作，为了便于理解，将代码简化如下，并把先关的函数都放在一起。其中，NormalisationFactor在论文中没有提及，也不太清楚这段代码的含义，大概就是在做归一化操作。

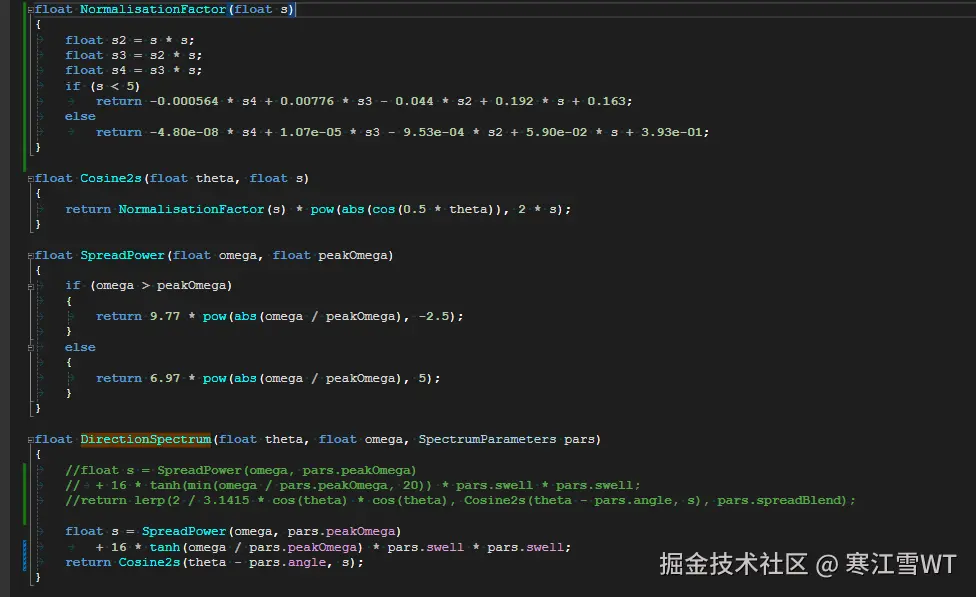
  这部分代码，有一个地方与论文中的公式不一致，如下图，发现这里是写反了。在调试时，修正后发现影响不大，可能是由于$\xi^2$太小导致的。

  $\theta$的计算如下图所示，直接代入k进行计算。

短波过滤（Short Waves Fade)

  短波过滤是最后一项因子。其公式如下：

$$s_{wave}(\vec{k},f)=\exp(-(f|\vec{k}|)^2)$$

  其中$f$是一个很小的值，代码中取值为0.01。当该值变大时，会发现网格的波动变得越来越平整。

最终计算

  把输入参数代入上述公式计算之后，把结果相乘，并进行最终的计算，得到初始频谱$h_0(\vec{k})$。这里先看代码吧。

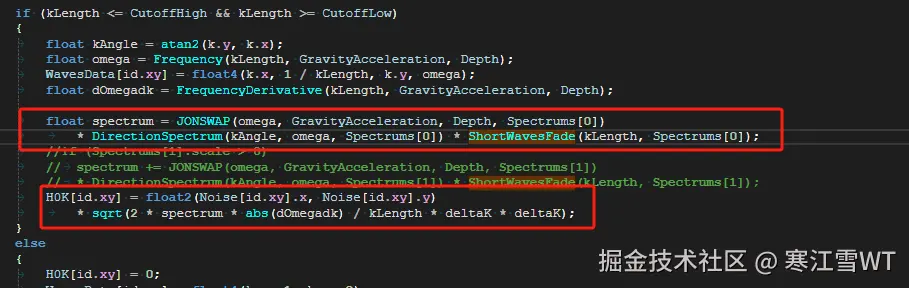
  可以看到这里有一个参数没有写出来，即deltaK。变量spetrum保存的结果，就是上述所有公式计算结果的乘积，将最后开根号的结果与噪声值相乘，保存为$h_0(\vec{k})$。最终的公式如下：

$$h_0(\vec{k})=noise.xy\sqrt{\frac{4\pi \cdot spetrum \cdot |d\omega_k|}{|\vec{k}|LengthScale^2}}$$

  有了$h_0(\vec{k})$之后，然后是计算$h_0^*(\vec{k})$。计算方法如下，这里特别注明的是，对H0的采样坐标有特殊的计算。

|$\vec{k}$|的范围限制

  基于JONSWAP公式模拟的海面，需要限制|$\vec{k}$|的范围。只在一定范围内生成数据，在范围之外直接填零。同时，还要将$\vec{k},\omega$保存到贴图中，供后续计算瞬时频谱时使用。这里需要特别注意的是，在范围之外的点，将|$\vec{k}$|保存为1。

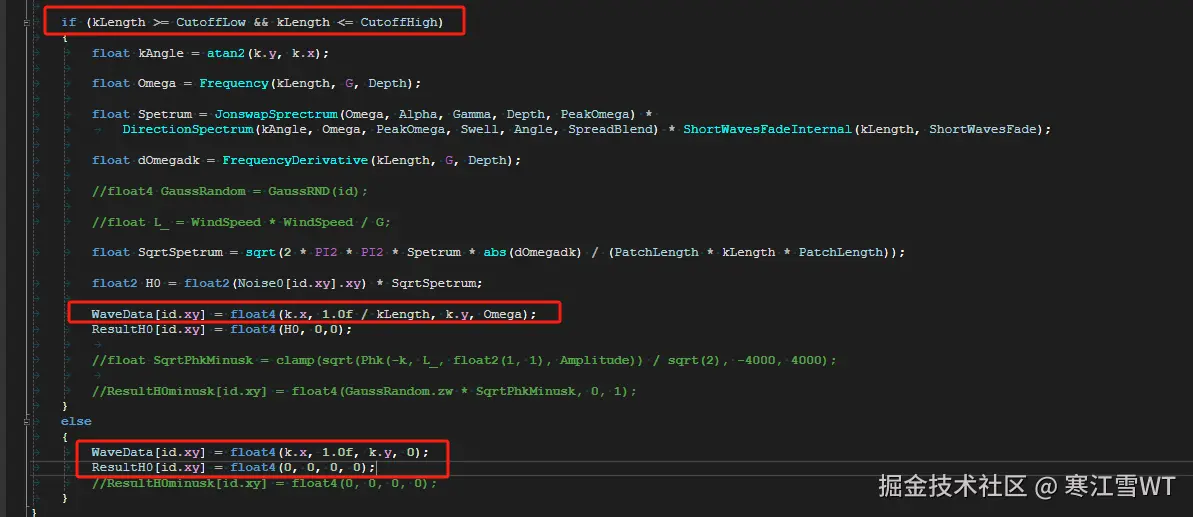
  范围的计算与LengthScale相关，每一级LOD使用的LengthScale都不同。代码如下：

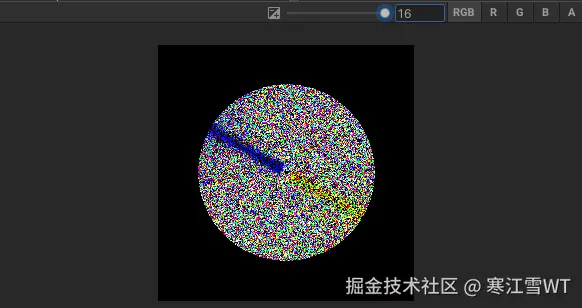
初始频谱效果

  如果按示例代码生成的初始频谱，应该如下图所示，需要特别说明的是，这是放大后的结果，否则看不到像素颜色。

生成初始频谱的代码

  上述所有过程，除了参数配置之外，都在ComputeShader中完成。在WavesCascade.cs中，可以看到这里对ComputeShader进行了两次调用。第一次是计算$h_0(\vec{k})$，第二次是计算$h_0^*(\vec{k})$

瞬时频谱$h(\vec{k},t)$的生成

  瞬时频谱的计算过程定义在TimeDependentSpectrum.compute，该过程与上一篇介绍的海面模拟过程一致。不过这份代码计算了更多的内容，我直接标注在代码中，就不介绍了。如果不关心渲染结果，只做海面网格的顶点扰动，可以只看Dx_Dz及Dy_Dxz这两张贴图。

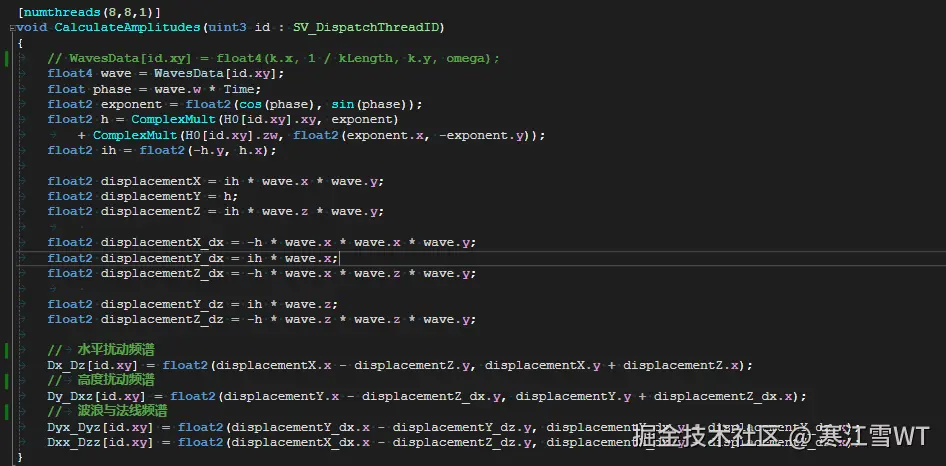
  有了这些数据之后，对这些数据执行IFFT，可以得到最终的数据。

贴图合并

  贴图合并的过程，定义在WavesTexturesMerger.compute中。该过程主要将前面IFFT的结果，合并程三张贴图，标注如下。

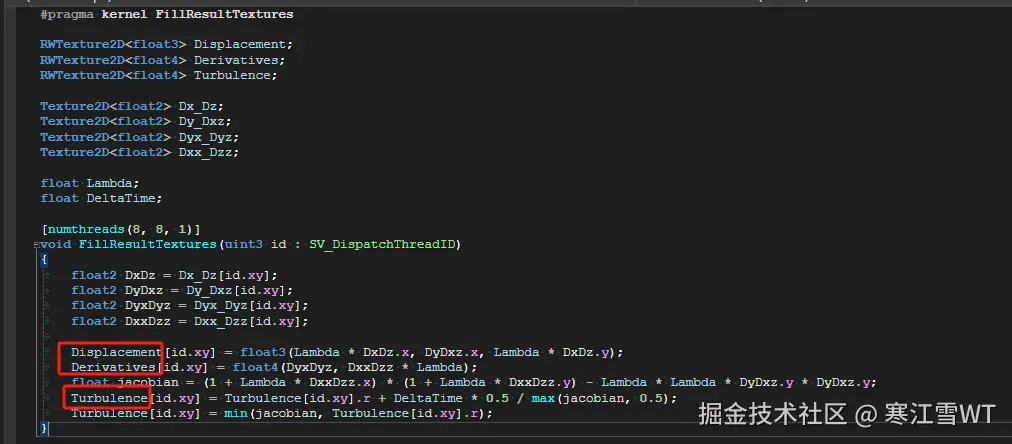
  第一张是顶点偏移贴图(Displacement)，被用来对海面网格顶点进行扰动。第二张是Derivatives，被用来计算法线，在片元着色器中使用。第三个是Turbulence，用来模拟浪尖，也是在片元着色器中使用。

本章小节

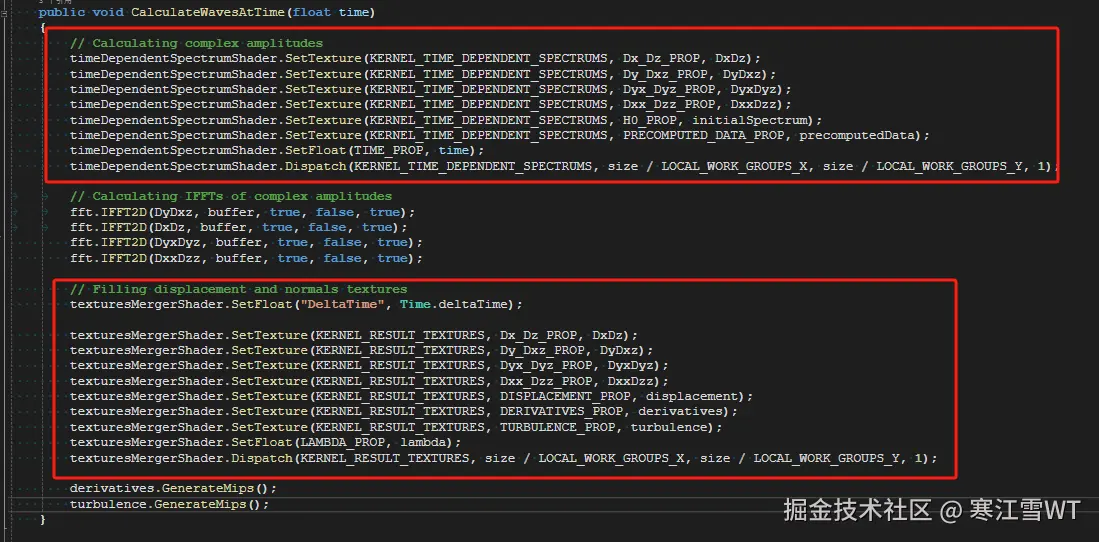
  贴图合并和瞬时频谱的计算是一起的，在WavesCascade.cs中定义，如下图所示的方法中，先计算了瞬时频谱，然后再进行贴图合并。

整个海浪模拟的过程

  整个海浪模拟的过程定义在WaveGenerator.cs中。

  在初始化时，创建了三个WavesCascade类，定义在WavesCascade.cs中，然后计算初始频谱。

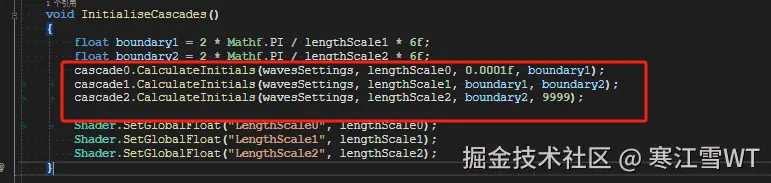
  在每一帧更新时，计算瞬时频谱，并合并贴图。

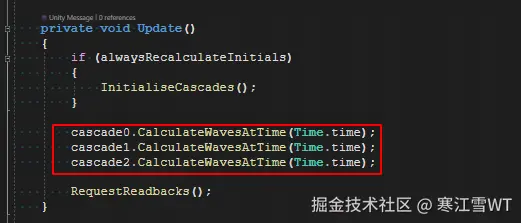
  纵观整个过程，这里模拟了三个不同LengthScale的波。在渲染时根据不同的LOD层级，叠加不同的波，得到看起来比较自然的效果。

渲染

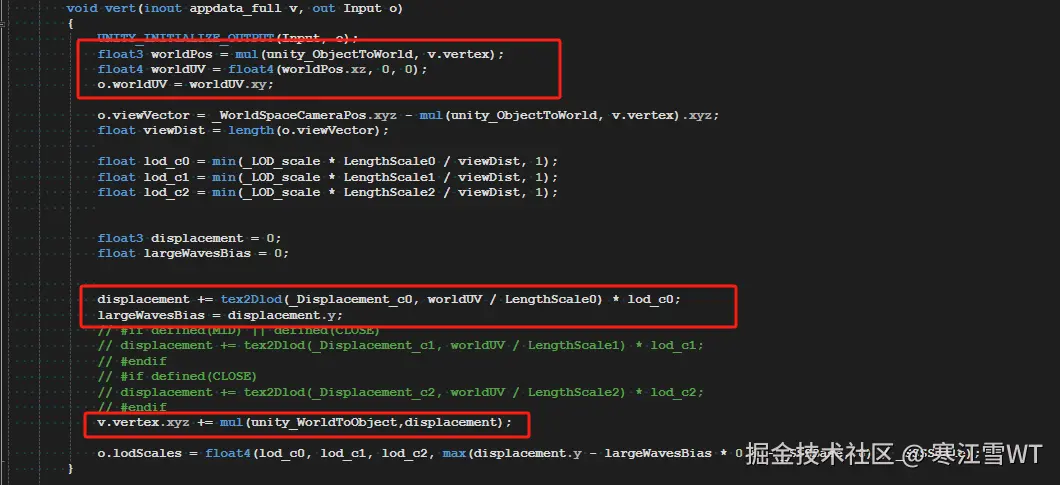
  关于海面网格的渲染，和上一篇一样，只展示对Displacement的采样。采样的UV坐标是与顶点的世界坐标有关。而后续具体的渲染方法说不上一二，就不过多介绍了。

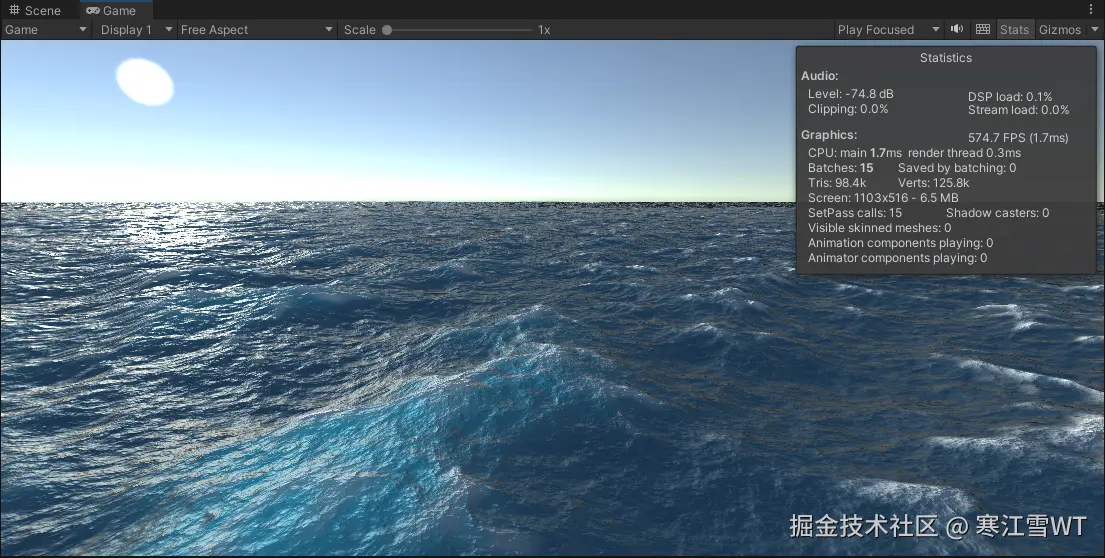
  最终生成的效果如下图所示：

总结

  终于到了该系列文章的尾声。之所以想做这一系列内容，一个是因为还大学时欠下的债——FFT相关内容。二个是在学生时代，由于水面模拟没有做出来，受制于FFT，导致最后更换了研究课题，所以这部分内容一直是想尝试做。在朋友的指导下，对FFT的内容有了一个初步的理解，在网上找了很多资料学习，才克服了这个障碍，所以索性就做一个系列的内容。另外还有一个小动机是，网上的资料太散太杂，也算是为后来者铺平道路。

参考文献和资料

[1] Horvath C J .Empirical directional wave spectra for computer graphics[C]//Symposium.2015.DOI:10.1145/2791261.2791267.

[2] GitHub链接

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以邮件