最小覆盖圆解决的问题是在平面上有n个散点。计算一个半径最小的圆能 包含所有的点。在网上搜索相关资料,在文章的最后列举一些参考的资料。
随机增量法解决最小覆盖圆的问题
对于一系列散点的最小覆盖圆,它满足如下性质,其中第二条性质和第三条性质必须满足其一。
存在且唯一
圆上有三个点集中的点
点集中有两个点是圆的直径
那么根据这些规律,如果已经计算出前$i-1$个点的最小圆,在加入第$i$个点后,最小圆有以下几种情况:
- 前$i-1$个点的最小圆(包含第$i$个点的情况)
- 前$i-1$个点中的两个点与第$i$个点确定的圆
- 前$i-1$个点中的一个点与第$i$个点作为直径的圆
增量法计算最小覆盖圆的过程,就是不断地加点,然后根据新加的点是否在圆内,当不在圆内时重复定圆。
在不考虑只有一个点,两个点的边界情况。算法流程描述如下:
输入n个点
随机打乱顶点在数组中的位置(为了获得更好的时间复杂度)
由顶点$P_0$和$P_1$计算最小圆$C(A)$
枚举顶点$P_2$-$P_n$,对于$P_i$作如下判断
- $P_i$在$C(A)$内,则$C(A)$不变,继续下一个点,否则进行下一步
- 计算$P_0$和$P_i$为直径的圆,记为$C(i)$,枚举点$P_1$到$P_{i-1}$,对于$P_j$作如下判断
- 顶点$P_j$在圆$C(i)$内,则$C(i)$保持不变,继续下一个顶点,否则进行下一步
- 计算$P_j$和$P_i$为直径的圆,记为$C(j)$。然后枚举顶点$P_0$到$P_j-1$,对于对于$P_k$作如下判断
- $P_k$不在圆$C(j)$内时,则更新$C(j)$为$P_i$,$P_j$和$P_k$构成的圆。
- 枚举完$P_k$之后,更新$C(i)$为$C(j)$
- 枚举完$P_j$之后,更新$C(A)$为$C(i)$
在Unity上使用C#的实现如下,会有一定的GC,但都能通过其他技巧优化。
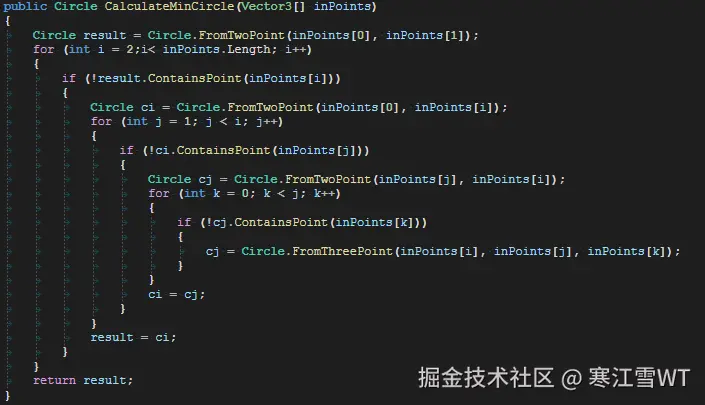
关于两点作为直径计算一个圆
这个比较简单,就是两点坐标相加乘以0.5,半径为距离的一半。

关于三点定圆的公式
这个问题会比上面的复杂一点,不过是可以推导出计算公式,这里就不推了。直接抄吧。
圆心坐标就是上面的公式,半径就是取其中一个输入的顶点,计算其与圆心的距离
